Šįkart papasakosiu jums apie vieną astronominių tyrimų aspektą, kuris dažnai lieka nesuprastas mėgėjų ir priveda prie nelabai prasmingos visos astronomijos, kaip mokslo, kritikos. Jis kažkiek susijęs su jau senokai mano minėtais paprastumo masteliais, bet tuo pačiu yra savitas dalykas. Visą reikalą trumpai apibūdina įrašo pavadinimas – tikslūs skaičiai astronomijoje nesvarbūs – tačiau kad tą suprastumėte, paaiškinsiu ir plačiau.
Štai praeitą savaitę buvo pranešta, jog po 4 milijardų metų susijungs Paukščių Takas ir Andromedos galaktika. Tarp komentarų įvairiose žiniasklaidos priemonėse, žinoma, buvo ir tokių: „O tai gal po 3 999 999 999 metų iš tikro, o ne po 4 milijardų?“ Kitais atvejais (pavyzdžių dabar nerandu, bet tikrai esu matęs) komentatoriai kimba prie žodžių „maždaug“ ir sinonimų, esančių straipsniuose. Jiems mat reikia tikslumo, o jei tikslumo nėra, tai ir visas tyrimas nieko vertas. Ir toks požiūris, bent jau internetuose, atrodo, toli gražu nėra išimtis. Gal ne visai taisyklė, bet netoli to.
Bet pažiūrėkime į visa tai iš mokslinės pusės. Atlikus bet kokį skaičiavimą, bet kokį tyrimą, gaunamas rezultatas turi tam tikrą, baigtinį, tikslumą. Galutinis atsakymas, jei gali būti išreikštas skaičiais (tiksliuosiuose moksluose dažniausiai gali, nors skaičiai ne visada yra svarbiausia dalis), turi ir kažkokią paklaidą. Priklausomai nuo srities ir nuo tyrimo, ta paklaida gali būti ir labai maža, ir labai didelė. Inžinerijoje ar kvantinėje mechanikoje rezultatas, kurio paklaida siekia keletą procentų, gali būti pražūtingas arba tiesiog visiškai nieko nesakantis. Tačiau astronomijoje keleto procentų paklaida dažnai yra labai maža, ir netgi rezultatai, nurodantys tik kokių nors objektų/reiškinių eilės dydį, yra reikšmingi. Taip yra dėl keleto priežasčių.
Pirma priežastis – astronomai tyrinėja ypatingai kompleksinius procesus. Pavyzdžiui žvaigždėdaros intensyvumas galaktikoje priklauso nuo galaktikos dydžio, dujų kiekio joje, dujų cheminės sudėties, magnetinio lauko stiprumo, turbulencijos, lėtų perturbacijų ir taip toliau. Tiksliai įvertinti kiekvienos sudėtinės dalies poveikį yra praktiškai neįmanoma. Net jei ir būtų įmanoma, visada labai pravartu suprasti atskirų dalių svarbą, taigi tyrinėti problemą, pasirinkus kažkokius parametrus kitiems įtakos šaltiniams ir koncentruojantis tik ties vienu ar pora. Šitaip gaunami rezultatai gali praturtinti supratimą apie procesų sąveikas (pavyzdžiui žvaigždėdaros spartos priklausomybę nuo dujų tankio galaktikoje; tokia yra žinoma iš stebėjimų, vadinama Kenikuto-Šmito dėsniu), tačiau konkretūs skaičiai gali kisti sąlyginai didelėse ribose, priklausančiose nuo kitų parametrų kitimo ribų.
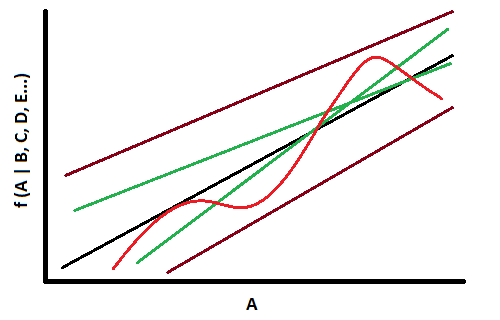
Antra priežastis šiek tiek susijusi su pirmąja. Astronomijoje darant tyrimus susiduriame su dviem problemomis: negalime išmatuoti labai tikslių dydžių bei negalime matyti procesų eigos. Matavimų paklaidos atsiranda dėl įvairių priežasčių, nuo instrumentų pajėgumų iki tų pačių aukščiau minėtų įvairių įtakos šaltinių. Procesų eigos nematome todėl, kad jie vyksta per lėtai. Iš viso šito seka, kad stebėjimų rezultatai yra lipdomi iš gabaliukų, reprezentuojančių skirtingas kokio nors proceso eigos stadijas. Pavyzdžiui, galaktikų evoliucijos skirtingų etapų trukmes nustatome iš to, kokia dalis matomų galaktikų yra kiekvienoje stadijoje (čia labai supaprastintas paaiškinimas, bet esmė panaši). Kiekvienas taškas mūsų supratimo kreivėje priklauso nuo tų visų paklaidų. Taigi teoriniuose modeliuose naudodami kažkokius stebėjimų duomenis, negalime gauti tikslesnių atsakymų, nei stebėjimų rezultatų tikslumas.
Procesų sekuliarumas svarbus ir dėl kito dalyko. Daugeliu atvejų astronomijoje nagrinėjami procesai yra tokie lėti, o objektai ir atstumai – tokie didžiuliai, kad didesnis skaičių tikslumas tiesiog neduoda jokios naudos. Net jei galėtume labai tiksliai nustatyti, kad Paukščių Takas su Andromeda susilies ne po keturių, o po 3,856011 milijardo metų, nuo to praktiškai niekas nepasikeistų. Tai vis tiek būtų reiškinys, įvyksiantis tolimoje ateityje; tokioje tolimoje, kad mums ją suvokti nėra galimybių.
Galiausiai astronomijoje labai retas procesas turi aiškią pradžią ir pabaigą, o objektas – kraštą. Turbūt aiškiausia riba yra žvaigždės gyvenimo pabaiga (kolapsas į baltąją nykštukę ar supernovos sprogimas), o visi kiti procesai – žvaigždžių gimimai, planetų formavimasis, Visatos plėtimasis – vyksta tolygiai, be labai staigių pokyčių, kurie leistų nubrėžti tikslią ribą. Taigi kalbėdami apie tų pačių Paukščių Tako ir Andromedos susiliejimą, galime pasakyti, kad susiliejimas prasidės maždaug po pustrečio milijardo metų, o dvi galaktikos viena taps po maždaug keturių. Tačiau ta viena galaktika dar kokį pusę milijardo metų bus akivaizdžiai neseniai susiliejusi, o prieš susiliejimo pradžią galaktikų pakraščiai patirs potvyninių jėgų sukeltas perturbacijas. Vadinasi nei tiksliai apibrėžtos pradžios, nei pabaigos, procesas neturi. Ir taip yra visur.
Nepaisant visų šių problemų, neleidžiančių nustatyti tikslių skaičių astronomijoje, jie kartais visgi yra svarbūs. Nuo žvaigždės masės labai priklauso jos likimas, taigi neužtenka žinoti tik jos eilės dydį. Dujų temperatūrai pakilus iki 3000 laipsnių, vandenilis tampa jonizuotas, taigi smarkiai pasikeičia jo optinės ir elektrinės savybės – vėlgi ryškus skirtumas. Tokiais atvejais skaičių tikslumas šį tą reiškia. Bet jų pasitaiko ne taip jau dažnai.
Taigi kai kitą kartą kas nors jums bandys aiškinti, kad astronomai nieko nesupranta ir nežino, nes pateikia skaičius su daug procentų paklaidomis, galėsite jiems paaiškinti, kas yra kas.
Laiqualasse

Tiksliai. Vieną pastraipą vagiu net ne astronominėms reikmėms :) .
Kurią ir kokioms, jei ne paslaptis? :)
Mano komentaras butu, jog tokiu dalyku kurie vyksta beprotiskai dideleje Visatoje tiksliai ismatuoti beveik neimanoma. Vien del to kad turetu buti nesaliskas stebetojas. Ir beje, Chaoso nuspeti neimanoma. :)
Taip, mūsų, kaip stebėtojų, netobulumas yra viena iš priežasčių, kodėl stebėjimai netikslūs.
Taigi kai kitą kartą kas nors jums bandys aiškinti, kad astronomai nieko nesupranta ir nežino, nes pateikia skaičius su daug procentų paklaidomis, galėsite jiems paaiškinti, kas yra kas.
Aš netgi sakyčiau, jog kaip tik verta atsargiai žiūrėti į tuos, kurie pernelyg tiksliai ir tvirtai kažką į priekį prognozuoja :). Ir nebijoti tų, kurie nevengia atvirai pripažinti paklaidos.
Irgi visiška tiesa. Kažkur esu skaitęs frazę, jog „kuo tikslesnis skaičius, tuo jis mažiau tikslus” ar kažkaip panašiai. Labai teisingas pastebėjimas, ypač astronomijoje.
Aha, šituo vadovaujuosi dar nuo tada, kai apie paklaidas nebuvau mokiusis, intuityviai turbūt.
Gera intuicija :)