Prieš maždaug mėnėsį Delfyje ir Technologijose (greičiausiai ir kitose vietose) pasirodė straipsnis, pavadinimu "Žemės centre – nesvarumas?". Jame trumpai papasakota apie tai, jog jei galėtume nusileisti gilyn į Žemės gelmes, tai kuo giliau leistumėmės, tuo silpnesnė būtų gravitacija, o galiausiai pačiame centre išvis beveik nesvarūs būtume. Šis faktas žinomas jau daugiau nei tris šimtmečius, bet neabejoju, kad pirmą kartą išgirdus gali pasirodyti keistas. Tad nekeista, kad ir komentaruose įvairių abejonių buvo išreikšta. Skaitydamas jau aštuonis puslapius straipsnio komentarų technologijose.lt, pagalvojau, kad gal visai įdomu būtų aprašyti šitą reiškinį detaliau, su įrodymais ir panašiai. Pasistengsiu viską pristatyti suprantamai "paprastiems mirtingiesiems", o tose vietose, kur bus daug detalių matematinių ar geometrinių išvedžiojimų, pridėsiu perspėjimų, kad galėtumėte ir neskaityti :)
Pradėkime… ne, ne nuo istorijos, kaip paprastai mano rašiniuose, bet nuo tokio uždavinio. Įsivaizduokime, kad turime mažą rutuliuką ir didelę (gerokai už tą rutuliuką didesnę) labai ploną sferą. Priminsiu, kad sfera – tai tuščiaviduris rutulio formos objektas; rutuliu vadinamas pilnaviduris analogas. "Labai plona" reiškia, kad į sferos paviršiaus storį galime neatsižvelgti. Sferos paviršinis tankis yra vienodas visuose jos taškuose; tai reiškia, kad sferos masė lygi jos paviršiaus plotui, padaugintam iš to tankio, o kiekvieno atskirai paimto jos gabaliuko masė yra lygi to gabaliuko plotui, padaugintam iš to paties tankio. Įdėkime rutuliuką į sferą (nesigilinkime, kokiu būdu) ir sistemą patalpinkime vakuume, toli nuo bet kokių kitų objektų, taip, kad sąveikautų tik jie du tarpusavyje, ir tik gravitaciškai. Klausimas – kokia jėga sfera veikia rutuliuką ir kaip tas rutuliukas judės?
Trumpas ir labai kokybinis (t.y. nenaudojantis skaičių) atsakymas – nesvarbu, kuriame taške sferos viduje rutuliukas bus, suminė jį veikianti jėga lygi nuliui. Kodėl? Įsivaizduokime, kad sferą padaliname į dvi dalis bet kokia plokštuma, einančia per rutuliuką. Greičiausiai tų dalių plotai, taigi ir masės, skirsis. Tačiau didesnioji sferos dalis yra toliau nuo rutuliuko, nei mažesnioji. O gravitacinė traukos jėga silpsta, didėjant atstumui tarp sąveikaujančių objektų. Ir taip jau išeina (įrodymas žemiau), kad vidutinis atstumas iki mažesniosios sferos dalies yra būtent tiek mažesnis, nei iki didesniosios, kad jų sukuriamos traukos jėgos yra vienodo dydžio. Tos jėgos nukreiptos priešingomis kryptimis, taigi jų atstojamoji (= vektorinė suma) yra lygi nuliui. Šis balansas nepriklauso nuo sferą dalinančios plokštumos krypties, vadinasi kurią kryptį benagrinėtume, rutuliuką veikiančių jėgų atstojamoji lygi nuliui. Vadinasi ir visų jėgų atstojamoji lygi nuliui, taigi rutuliukas niekur nejudės.
Dabar – kiekybinis matematiškas įrodymas. Jei matematika jums baisi, galite iškart peršokti keliomis pastraipomis žemyn (ten, kur pajuodinta). Įsivaizduokime , kad pro rutuliuką nubrėžiame tiesę, o tada – du kūgius, kurių kampai prie viršūnės yra vienodi, viršūnės sutampa su rutuliuku, o ašys – su ta tiese. Kūgiai plečiasi į priešingas puses nuo rutuliuko, ir abu kerta sferą. Jei žiūrėtume į šitokios sistemos projekciją dvimatėje erdvėje, matytume tris tieses, susikertančias ties rutuliuku (dvi tiesės yra kūgio kraštų projekcijos, trečioji – kūgio ašis). Žiūrint iš rutuliuko padėties, kiekvienas kūgis "rėmina" vienodą erdvinį kampą Omega = 2*pi*(1-cos(a)); čia a yra pusė kūgio kampo prie viršūnės. Sferinė geometrija mums teigia, jog erdvinis kampas dOmega (čia d reiškia diferencialą, arba labai mažą dydį) R spindulio sferos paviršiuje atitinka paviršiaus plotą R^2*dOmega. Vadinasi jei atstumai nuo rutuliuko iki kūgių susikirtimų su sferos paviršiumi yra R1 ir R2, tai atitinkami kūrgių pagrindų plotai, statmeni jų ašies tiesei, yra R1^2*dOmega ir R2^2*dOmega.
Rutuliukas bendru atveju nėra sferos centre, taigi linija, einanti pro rutuliuką, sferą kerta ne stačiu kampu. Tačiau svarbu yra tai, kad ir viename, ir kitame susikirtimo taške šis kampas yra vienodas. Tą įrodyti galima šitaip: bet kokia atkarpa, einanti tarp dviejų sferos paviršiaus taškų, yra vadinama styga. Nubrėžkime sferos spindulį, kertantį šią stygą statmenai (tas spindulys neeis per rutuliuką, bet tai nesvarbu). Toks spindulys stygą dalina į dvi vienodo ilgio dalis (šios teoremos čia neįrodinėsiu, bet tiesiog nusibraižius schemą pakankamai aišku turėtų būti). Taip pat nubrėžkime du sferos spindulius iki taškų, kuriuose styga kertasi su sfera. Taip gauname du trikampius, kurių kiekvieną sudaro spindulys iki susikirtimo taško, pusė stygos ir spindulio atkarpa nuo stygos iki centro. Spinduliai yra vienodi, stygos abi pusės vienodo ilgio, atkarpa nuo stygos iki centro bendra abiems trikampiams. Na o du trikampiai, turintys po tris vienodo ilgio krašines, yra vienodi, vadinasi ir jų visi kampai vienodi. Taigi vienodi ir kampai tarp stygos ir abiejų spindulių ties susikirtimo taškais. Taigi bet kokia sferos styga jos paviršių abiejose pusėse kerta vienodu kampu.
Ką tai bendro turi su rutuliuku ir jį veikiančiomis jėgos? Ogi tai, kad tų kūgių su viršūnėmis ties rutuliuku, "atkertami" sferos paviršiaus gabaliukų plotai yra R1^2*dOmega/cos(b) ir R2^2*dOmega/cos(b), kur b yra tas aukščiau minėtas kampas tarp kūgio ašies (=stygos) ir sferos paviršiaus. Dabar atsiminkime, jog sferos gabaliuko masė yra lygi to gabaliuko plotui, padaugintam iš tankio, o tankis lygus visoje sferoje. Vadinasi, tų gabaliukų masė bus M1 = A*R1^2 ir M2= A*R2^2; čia raide A pažymėjau visus kitus dauginamuosius, kurie yra tik konstantos.
Dabar prisiminkime Niutono suformuluotą visuotinės traukos dėsnį: F = -GMm/r^2. Čia F yra jėga, G – gravitacijos konstanta, M ir m – sąveikaujančių objektų masės, r – atstumas tarp objektų. Minuso ženklas reiškia, kad objektai traukia vienas kitą. Mūsų nagrinėjamu atveju, M yra sferos gabaliuko masė, m – rutuliuko masė, r lygus R1 arba R2. Matome, kad M yra proporcinga R^2, tad padalinus iš R^2 lieka konstanta. Vadinasi rutuliuką veikianti vieno sferos gabaliuko jėga nepriklauso nuo atstumo iki tarp rutuliuko ir to sferos gabalo. Kadangi tokie gabaliukas yra du ir traukia priešingomis kryptimis, jų jėgos kompensuojasi ir rutuliuką veikianti jėga lygi nuliui. O kadangi šis sprendimas nepriklauso nuo per rutuliuką nubrėžtos linijos krypties (bet kuri linija kirs sferą dviejuose taškuose), taigi jis galioja bet kuriai krypčiai. Vadinasi bet kuria kryptimi rutuliuką veikiančių jėgų atstojamoji lygi nuliui, taigi rutuliukas niekur nejudės.

Pirmosios (ir antrosios) Niutono teoremų iliustracija elektromagnetizmo atveju. Šiuo atveju gravitacinė ir elektromagnetinė sąveikos visiškai nesiskiria viena nuo kitos, taigi iliustracija tinka ir tekste aprašomam atvejui.
Matematika (kol kas) baigta, galite skaityti toliau. Šis teiginys yra vadinamas pirmąja Niutono teorema. Taip taip, Niutonas ne tik tris garsiuosius dėsnius suformulavo, jis iš jų dar ir tris teoremas išvedė ir įrodė. Beje, Niutono laikais teoremos įrodymui užteko nubraižyti apskritimą ir keletą tiesių jame, ir daugumai būdavo aišku, apie ką eina kalba ir kas iš to gaunasi… O šiaip teoremą įrodyti šiek tiek lengviau (t.y. užima mažiau rašymo) skaičiuojant ne gravitacines jėgas, bet gravitacinius potencialus ir parodant, kad visame sferos viduje potencialas yra vienodas. O jei potencialas vienodas, tai ir jėgų nebus, nes jėga susidaro tik ten, kur yra potencialų skirtumas (visiškai analogiškai srovė elektros grandinėje teka tik ten, kur yra įtampų, t.y. elektrinių potencialų, skirtumas).
Verta atsiminti, kokios prielaidos reikalingos, kad ši teorija būtų teisinga. Visų pirma, ji galioja tik labai specifinių kūnų viduje. Aukščiau pateiktas įrodymas tinka sferai (= vienodo spindulio visomis kryptimis kūnui), tačiau taip pat ši teorema galiojai ir geometrinei figūrai, vadinamai homoeoidu (tariama ho-mo-e-oi-das, jei ką). Tai yra burbulas, kurio tankis (ne paviršinis, o tūrinis) yra vienodas, o vidinis ir išorinis paviršiai – vienodo ekscentriškumo (~ eliptiškumo) sferoidai. Daugmaž galite įsivaizduoti dvi elipses, kurių eliptiškumas (t.y. "suplojimas", lyginant su apskritimu) vienodas bei vienodi centrai, tik dar išsuktas į trimačius kūnus. Taip pat svarbu tai, kad sferos (ar homoeoido) tankis privalo būti vienodas.
Iš kitos pusės, nykstamai mažas sferos storis reikalingas tik tam, kad būtų lengviau įrodyti teoremą ir kad galėtume išvesti bendresnį atvejį. Įsivaizduokime nebe vieną sferą, bet daugybę įvairaus tankio (tik vis dar vienodo kiekvienai sferai atskirai) plonyčių sferų, kurios sudėtos viena į kitą, kaip kokios matrioškos. Jei į tokios sistemos vidų įdėtume rutuliuką, jis būtų kiekvienos iš šių sferų viduje. Vadinasi, kiekvienos sferos gravitacija visiškai kompensuotųsi ir rutuliukas vis tiek nejudėtų. Taigi pirmąją Niutono teoremą galima apibendrinti šitaip: bet kokio sferiškai simetriško burbulo viduje esantis kūnas nejaučia jokios gravitacinės traukos, kuri būtų sukuriama to burbulo masės. Lygiai tas pats galioja ir homoeoidams – jei sudedame daugybę jų vieną į kitą, viduje esantis kūnas traukos nejunta.
Supratę šiuos dalykus, galime pereiti prie antrosios Niutono teoremos. Ši teorema teigia, jog kūnas, esantis sferiškai simetriško objekto išorėje, pastarojo gravitacinę trauką jaučia taip, lyg visa to objekto masė būtų sukoncentruota objekto centre ir pats objektas būtų taškinis kūnas. Šios teoremos įrodymą kokybiškai pristayčiau šitaip. Nubrėžkime tiesę per tiriamą kūną ir sferiškai simetriško objekto centrą. Akivaizdu, kad bet kokia plokštuma, einanti per šią tiesę, objektą dalina į dvi lygias dalis. Vadinasi objekto trauka į bet kurį šoną nuo centro kompensuojasi ir traukos jėga tikrai yra nukreipta į objekto centrą. Tam, kad įrodytume, jog tos jėgos dydis yra tiksliai toks, koks būtų, jei visa objekto masė būtų sukoncentruota centre, jau reikia matematikos. Tačiau bent jau kokybiškai galima įsivaizduoti, kad paimame sferos gabaliukus ir juos perkeliame vieną po kito į centrinį tašką. Kai kurie gabaliukai nuo tiriamojo kūno nutols, kai kurie – priartės. Ir vėlgi taip išeina, kad nutolstančių gabaliukų traukos sumažėjimą visiškai kompensuoja priartėjančių gabaliukų traukos padidėjimas.
Dabar vėl bus daug matematikos, taigi galite leistis žemyn iki pajuodinto teksto. Taigi, pagalvojus kokybiškai, reikia suskaičiuoti ir kiekybinę išraišką. Tą galima būtų padaryti naudojant panašų būdą, kaip ir įrodant pirmąją teoremą – nubrėžti daug linijų ir kūgių nuo tiriamojo kūno pro sferą, skaičiuoti jų gravitacinę sąveiką ir t.t. Bet paprasčiau tą padaryti šiek tiek kitaip (šis būdas pristatytas ir Vikipedijoje, ten net animuoti paveiksliukai yra). Suskaidykime sferą į daugybę juostų, kurių kiekvienos storis yra R*dTeta (Teta šiuo atveju yra graikiška raidė, o ne vieno iš tėvų sesuo; ir kirtis ant pirmo skiemens), o spindulys – statmenas linijai tarp traukiamo kūno ir sferos centro. Kiekviena tokia juosta kūną traukia jėga F = -Gm(dM)/s^2*cos(Phi), kur s yra atstumas nuo kūno iki juostos, o Phi – kampas tarp šio atstumo ir linijos masės centro link. Išsireiškę masę randame, jog dM = M*sin(Teta)*d(Teta)/2. Tada panaudoję kosinusų teoremą ir suintegravę šią jėgos išraišką nuo s = r-R iki s = r+R, kur r yra atstumas iki masės centro, o R – sferos spindulys, gauname galutinę išraišką F = -GmM/r^2, t.y. tiksliai tokią, kokia būtų, jei visa sferos masė būtų sutelkta jos centre.
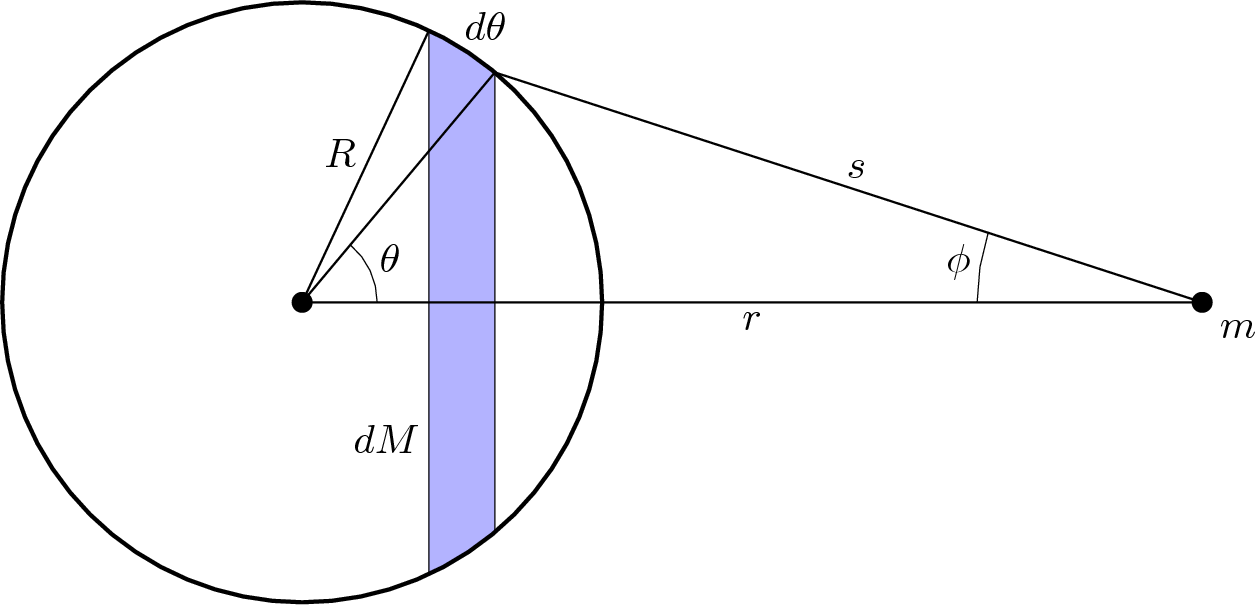
Diagrama antrosios Niutono teoremos įrodymui
Matematika baigėsi, galite skaityti toliau. Taigi, žinome, jog kūnui esant sferos išorėje, tos sferos trauka veikia taip, lyg visa jos masė būtų sutelkta sferos centre. Analogiškai kaip ir pirmosios Niutono teoremos atveju, bet kokį sferiškai simetrišką kūną galime suskaidyti į daugybę plonų sferų ir randame, kad bet kokio sferiškai simetriško kūno išorėje gravitacinė trauka yra lygi tokiai, kokia būtų, jei visa kūno masė būtų sutelkta jo masės centre.
Įrodžius ir atsimenant šias dvi teoremas, lengva įrodyti ir trečiąją. Ji skamba taip: vienodo tankio rutulyje gravitacija silpsta tolygiai, einant nuo jo paviršiaus iki centro, o centre visiškai išnyksta. Šios teoremos įrodymui pakanka suskaidyti tą rutulį į daugybę sferų, kurių visų tankis (šiuo atveju) vienodas. Esant kažkuriame taške rutulio viduje, pagal pirmąją Niutono teoremą, toliau nuo centro nutolusių sferų trauka pranyksta ir mums svarbios tiktai arčiau centro esančiosios. Jų trauką apskaičiuojame pagal antrąją Niutono teoremą: F = GMm/r^2. Tačiau masė M priklauso nuo atstumo r, nes mums svarbi tik rutulio dalis, esanti arčiau centro, nei r. Šios dalies masė lygi tankiui, padaugintam iš spindulio r rutulio tūrio: M = 4*pi/3*r^3*ro (ro – dar viena graikiška raidė, reiškianti tankį). Įstačius šią išraišką į jėgos formulę, gauname atsakymą F = 4*pi*G*ro*m*r/3, t.y. jėga tiesiogiai proporcinga r. Na o pačiame centre r = 0, taigi ir F = 0.
Kas iš viso to? Į Žemės gelmes taip giliai, kad pajustume gravitacijos mažėjimą, nelendame, kitokių sferų irgi lyg ir nedažnai sutinkame. Be to, net jei ten iki Žemės centro ir nukeliautume, šie teoriniai išvedžiojimai negaliotų, nes Žemė nėra sferiškai simetriška. Visgi keletą svarbių pasekmių šios teoremos turi. Pirmoji – kadangi Visata yra daugmaž izotropinė (t.y. vienoda visomis kryptimis, kitaip tariant, sferiškai simetriška), bent jau žiūrint didžiausiais masteliais, nereikia atsižvelgti į labai tolimų objektų gravitacijos įtaką. Antroji – jei matome, kad kažkas sukasi orbita, vadinasi tos orbitos viduje privalo būti traukiantis kūnas; ši išvada leidžia bene tiksliausiai nustatyti mūsų Galaktikos centre esančios supermasyvios juodosios skylės egzistavimo faktą ir parametrus. Galų gale, net jei kažkoks materijos pasiskirstymas yra tik apytikriai sferiškai simetriškas, jo kuriamas gravitacinis laukas bus panašus į visiškai sferinio kūno, tad teoremas galima naudoti bent jau kaip artinius realybei.
Dar viena, irgi gana teorinė, pastaba – nesvarumas rutulio centre nereiškia, kad ten nieko nėra ir viskas išskrenda kažkur tolyn. Jei iškastume tunelį nuo vieno ašigalio iki kito ir leistume jam užsipildyti oru, tai ties Žemės centru slėgis būtų milžiniškas. Taip yra todėl, kad slėgis priklauso nuo viso oro stulpo svorio, t.y. nuo bendro svorio visų molekulių, esančių tarp centro ir atmosferos viršaus. Parašius slėgio diferencialinę išraišką dP = ro*g*dr, kur ro yra atmosferos tankis (paprastumo dėlei jį galime laikyti nekintamu, nors realybėje darant tokį bandymą, oras giliai būtų suspaudžiamas, taigi slėgio vertė dar padidėtų), o g – laisvojo kritimo pagreitis (lygus traukos jėgai, padalintai iš traukiamo kūno masės), ir ją suintegravus, gaunama slėgio vertė Žemės centre yra maždaug 400 atmosferų! T.y. 400 kartų didesnis slėgis, nei ant Žemės paviršiaus. Panašus slėgis yra keturių kilometrų gylyje po vandeniu. Žodžiu be labai labai tvirto skafandro ten leistis nepatartina.
Šiuo perspėjimu ir užbaigsiu pernelyg matematišką įrašą. Jau galite atsibusti :)

Man kazkaip paskaicius kilo tokia keista mintis… O jei jau ishkasus ta tuneli iki zemes centro.. ir leidus uzpildyti ji oru.. Iki pat centro nuleistume stora tusciavidure zarna.. Ar oro slegis stumtu ora is tos zarnos iki pavirshiaus su didele jega? Gal tai gautusi amzinas variklis? :) Gi tunelio plotas butu gerokai didesnis nei zarnos, turetu veikti kaip turbina?
Amžinas variklis nesigautų, nes žarnoje, kaip ir tunelyje, nusistovėtų atmosferos slėgio gradientas – arti centro slėgis didesnis, arti paviršiaus – mažesnis.
Vien tik vakuumo neužtenka, kad išnyktu išorinė gravitacija.
Reikia tai atlikti TKS viduje, arba labai stipriai nutolus nuo Žemės ir nepriartėjus prie kitos planetos.
Nesu tikras, kas jums konkrečiai čia užkliuvo, bet apie išorinės gravitacijos išnykimą lygtai nieko nerašiau. Iš skirtingų pusių veikianti trauka kompensuojasi ir atstojamoji lieka lygi nuliui, bet tai nėra tas pats, kad gravitacijos pranykimas.