Astrofizika daugeliu atžvilgių yra nuostabi mokslo šaka – mes gilinamės į didžiausio masto kosmoso paslaptis, ekstremalius reiškinius, kurių Žemėje sutikti neįmanoma, tiriame planetų, žvaigždžių ir galaktikų kilmę bei vystymąsi, stebime milijardų metų praeitį ir prognozuojame analogišką ateitį. Bet šie stulbinantys aspektai kelia ir didelę problemą: astrofizika yra turbūt vienintelis gamtos mokslas, kuriame praktiškai neįmanoma atlikti eksperimentų. Čia mus lenkia ne tik chemikai ar biologai, bet netgi socialinių mokslų atstovai – kad ir kaip sudėtinga būtų tyrinėti žmones ir jų santykius, tą padaryti bent jau įmanoma. Tuo tarpu žvaigždės laboratorijoje nesukursi, milijonus metų trunkančių galaktikų pokyčių realiu laiku neišnagrinėsi. Kažkiek eksperimentai padeda astrochemikams, tyrinėjantiems, pavyzdžiui, chemines reakcijas tarpžvaigždinėje erdvėje, arba planetų tyrinėtojams, nagrinėjantiems jų paviršiaus savybių evoliuciją. Bet dauguma astronominių reiškinių yra per dideli, per lėti, ar kitaip pernelyg ekstremalūs, kad galėtume juos atkurti Žemėje.
Neturėdami galimybės eksperimentuoti ir nepasitenkindami vien stebėjimais, astronomai nuo senų laikų ieško kitų būdų, kaip tyrinėti kosmosą. Pagrindinis iš jų, padedantis susigaudyti milijardus metų trunkančiuose reiškiniuose, suprasti jų prigimtį, yra skaitmeniniai modeliai. Beje, jie taikomi toli gražu ne tik astrofizikoje – daugybė sričių, nuo jau minėtos biologijos iki inžinerijos ar filmų pramonės, šiais laikais neįsivaizduojamos be kompiuterinių modelių. Dažnai šie modeliai yra glaudžiai susiję arba išsivystę iš astronominių.
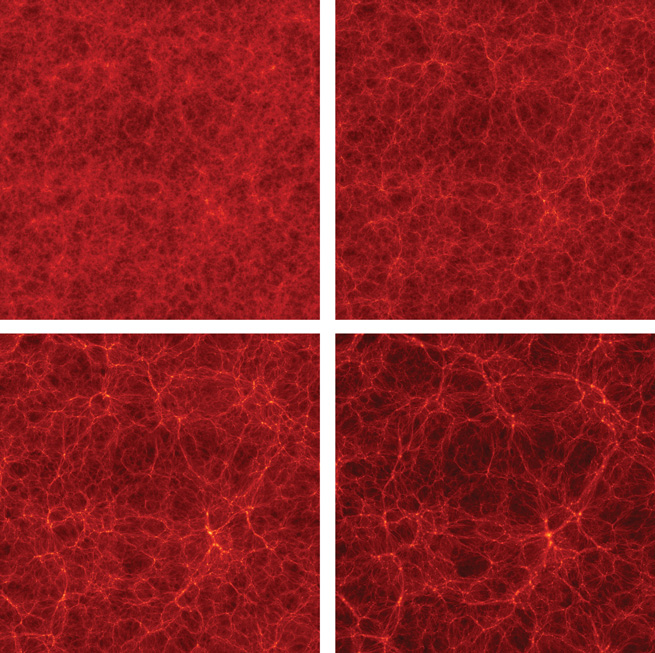
Kosmologinio skaitmeninio modelio Bolshoi rezultatai – kosminio voratinklio formavimasis. Spalvos šviesumas žymi tamsiosios materijos tankį: viršuje 500 mln. ir 2,2 mlrd. m. po Didžiojo sprogimo, apačioje 6 mlrd. m. po Didžiojo sprogimo ir šiandien. Šaltinis: modelis – Anatoly Klypin ir Joel R. Primack; vizualizacija – Stefan Gottlöber/Leibniz Institute for Astrophysics Potsdam
Šio pažintinio straipsnio nebūtų buvę, jei ne mano rėmėjai Patreon platformoje – ačiū jums! Jei manote, kad mano tekstai verti vieno-kito dolerio per mėnesį, paremti mane galite ir jūs.
Skaitmeniniai modeliai šiandien yra neatsiejami nuo kompiuterių – dažnai labai galingų skaičiavimų klasterių, sudarytų iš tūkstančių branduolių. Visgi jų ištakas galime rasti dar XVIII amžiuje, gerokai iki kompiuterių ar bet kokių skaičiavimo mašinų. Tada didysis matematikas ir kitų sričių mokslininkas Leonhardas Euleris sugalvojo metodą, kaip galima apytikriai išspręsti matematinių lygčių rūšį, vadinamą diferencialinėmis lygtimis. Šie uždaviniai, susieja kažkokios funkcijos vertę ir jos kitimo spartą. Kartais jas įmanoma išspręsti palyginus paprastai, bet kartais jos apskritai neturi tiksliai išreiškiamų sprendinių. Tokiu atveju apytikrį sprendinį galime rasti „žingsniuodami“ per funkciją nuo kažkokio pradinio taško, o žingsnio kryptį pasirinkdami pagal žinomą funkcijos kitimo spartą.
Toks ryšys tarp tolydžios – ties kiekvienu tašku vertę turinčios – funkcijos ir diskretaus – vertę turinčio tik tam tikrose vietose – jos sprendimo būdo yra be galo svarbus šiandieniniam skaitmeniniam modeliavimui. Mat kompiuteriai dirba tik su diskrečiais duomenimis, o tyrinėjamos sistemos dažniausiai yra tolydžios. Pavyzdžiui, laiko tėkmė yra tolydi, tačiau skaitmeniniame modelyje tenka ją pakeisti diskrečiais laiko žingsniais. Nuo Eulerio laikų metodai, kaip tą padaryti, patobulėjo, bet pats principas išlieka gana panašus.
Prie laiko žingsnių dar grįšime, o dabar verta susipažinti su pirmuoju skaitmeniniu astrofizikiniu modeliu, padarytu dar 1941 metais. Tada kompiuterių, kaip juos suprantame šiandien, dar nebuvo, bet kūrybingam švedui astrofizikui Erikui Holmbergui tai nesutrukdė. Lundo universiteto observatorijoje dirbęs mokslininkas didelėje salėje sudėliojo 74 lempas, iš jų suformuodamas dviejų galaktikų atvaizdus. Lempos šviesa, panašiai kaip ir gravitacija, nuo atstumo priklauso kvadratiškai: dvigubai toliau esantis šviestuvas atrodo keturis kartus blausesnis, kaip ir dvigubai toliau esantis kūnas traukia keturis kartus silpniau. Taigi lempų skleidžiamą šviesą galima prilyginti gravitacijos jėgai. Šitaip Holmbergas galėjo palyginus lengvai apskaičiuoti, kaip juda galaktikas sudaranti medžiaga, veikiama jų tarpusavio gravitacijos. Modelio rezultatai jam parodė, kad prasilenkiančios galaktikos dėl potvyninių efektų praranda tiek energijos, kad gali susijungti į vieną, o nuo tolimųjų jų pusių tolyn nusidriekia spiralinės vijos. Būtų atradęs ir daugiau esminių galaktikų susiliejimo proceso elementų, jei ne pasirinktas supaprastinimas, centrines penkiolika kiekvienos galaktikos lempų judinant kartu tarsi kietą kūną, o ne kiekvieną atskirai.
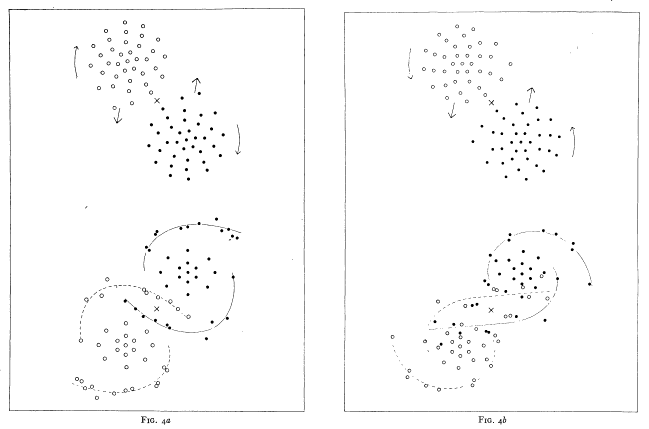
E. Holmbergo modelio rezultatai. Kairėje galaktikos sukasi priešinga kryptimi, nei skrieja viena aplink kitą, dešinėje – ta pačia. Viršutiniai vaizdai yra pradinės sąlygos, apatiniai – situacija po prasilenkimo; linijos vaizduoja reikšmingas struktūras. Šaltinis: Holmberg 1941, Astrophysical Journal
Holmbergo naudotame modelyje buvo skaičiuojamas tik vienos jėgos – gravitacijos – poveikis. Toks modelis vadinamas N-kūnų modeliu, nes jis sprendžia N-kūnų uždavinį, žinomą dar nuo Niutono laikų. Šis uždavinys skamba labai paprastai: žinodami kelių dangaus kūnų mases, pradines padėtis bei judėjimo greičius ir kryptis, norime nustatyti, kaip jie judės laikui bėgant, veikiami tarpusavio gravitacijos. Deja, uždavinys gražiai analitiškai – be skaitmeninių metodų – išsprendžiamas tik tada, kai kūnai yra du, pavyzdžiui dvinarė žvaigždė ar aplink žvaigždę skriejanti planeta. Jei kūnai yra trys, sprendiniai egzistuoja tik idealizuotais atvejais: kai kurioms labai nenatūralioms pradinėms konfigūracijoms arba tada, kai kūnų masių santykiai labai dideli. Tarkime, galime išspręsti, kaip juda palydovas, veikiamas Žemės ir Saulės, nes palydovo masė neturi pastebimos įtakos planetai ir žvaigždei. Arba galime išspręsti Mėnulio, Žemės ir Saulės sistemos judėjimą, nes galime jį išskaidyti į Mėnulio bei Žemės judėjimą aplink bendrą masės centrą ir to masės centro judėjimą aplink Saulę. Kai kūnų pasidaro dar daugiau, nebeįmanomi tampa ir idealizuoti sprendiniai – tenka pereiti prie skaitmeninių metodų.

Trijų kūnų uždavinio skaitmeninis sprendimas. Šiuo atveju sistema galiausiai pasidalina į dvinarę žvaigždę ir pavienį objektą. Šaltinis: Eltaurus @ Imgur
N-kūnų modelis konceptualiai yra gana paprastas ir lengvai skaitmenizuojamas. Sistemą sudarančių kūnų mases, padėtis ir greičius nurodyti kompiuteriui nesudėtinga, taip pat iš principo nesudėtinga apskaičiuoti ir kiekvienos kūnų poros tarpusavio trauką. Tuomet belieka susumuoti kiekvieną kūną veikiančias jėgas (nepamirštant, kad jos veikia skirtingomis kryptimis), apskaičiuoti kūno pagreitį ir galima įvertinti, kaip kiekvienas kūnas turėtų pajudėti per tam tikrą laiko žingsnį.
Žinoma, konceptualus paprastumas slepia ne vieną praktinę problemą. Aukščiau aprašytame modelyje jų yra keletas. Pavyzdžiui, labai svarbu, kokį laiko žingsnį parinksime: jei jis labai ilgas, gaunami rezultatai greitai nustos atitikti realybę; jei labai trumpas, skaičiavimai užtruks labai ilgai. Taip pat problema kyla dėl to, kad didėjant dalelių skaičiui, jų porų skaičius auga kvadratiškai: dvigubai daugiau dalelių turinčioje sistemoje porų yra keturis kartus daugiau. Taigi labai sparčiai auga skaičiavimo resursų sąnaudos. Per dešimtmečius, tobulinant modelius, sukurtas ne vienas būdas skaičiavimus optimizuoti.
Pagrindinis laiko žingsnių parinkimui svarbus rezultatas suskaičiuotas irgi prieš kompiuterių erą – trečiajame praeito amžiaus dešimtmetyje. Trys matematikai – Richardas Courantas, Kurtas Friedrichsas ir Hansas Lewy – nagrinėjo skaitmeninio lygčių sprendimo algoritmus. Jie apskaičiavo, koks gali būti maksimalus algoritmo žingsnis, kuris duoda „ne per didelį“ skaitmeninio sprendinio nuokrypį nuo tikrojo. Šis žingsnis priklauso nuo lygties vertės ir jos kitimo spartos. Paėmus konkretesnį pavyzdį – jei nagrinėjame kokią nors N-kūnų sistemą, laiko žingsnį reikia paimti tokį, kad dalelė per jį nuskristų gerokai mažesnį nuotolį, nei tipinis atstumas tarp jos ir kitų dalelių. Taip pat reikia atsižvelgti ir į greičio pokyčius – parinkti tokį laiko žingsnį, kad per jį labai reikšmingai nepasikeistų dalelės greitis.
Skaičiuodami daugelio dalelių sistemos evoliuciją greitai pastebėsime, jog skirtingoms dalelėms reikėtų parinkti skirtingus laiko žingsnius. Pavyzdžiui, jei mūsų sistema yra kamuolinis žvaigždžių spiečius, centre esančios žvaigždės juda žymiai greičiau ir didesniais pagreičiais, nei pakraščiuose. Skaičiuoti visų dalelių judėjimą tuo pačiu trumpu laiko žingsniu yra labai nepraktiška – be reikalo išnaudojami kompiuterio resursai. Bet ir čia turime sprendimą: skirtingas daleles galime judinti skirtingais laiko žingsniais. Tiesiog reikia, kad šių laiko žingsnių santykiai būtų dvejeto laipsniai: pavyzdžiui, jei trumpiausią laiko žingsnį prilyginame vienetui, tai kitų dalelių laiko žingsniai gali būti lygūs dviem, keturiems, aštuoniems ir taip toliau. Ir dar arti viena kitos esančios dalelės turėtų judėti panašiais – ne daugiau nei keturis kartus besiskiriančiais – laiko žingsniais.
Kamuolinį spiečių
galime panaudoti ir kaip pavyzdį jėgų skaičiavimo problemai
iliustruoti. Tokiuose spiečiuose dažniausiai yra nuo kelių
tūkstančių iki milijono žvaigždžių. Jei spiečiuje žvaigždžių
tūkstantis (![]() ), tai jų porų yra maždaug milijonas (
), tai jų porų yra maždaug milijonas (![]() ); milijonas ir skaičiuojamų jėgų. Dešimties tūkstančių
žvaigždžių spiečiuje jėgų skaičiuoti reikėtų jau šimtą
milijonų – šimtą kartų daugiau. Bet paimkime vieną konkrečią
žvaigždę ir panagrinėkime, kaip ją veikianti jėga priklauso nuo
kitų žvaigždžių padėčių. Jei truputį pakeistume arti
esančios kaimynės padėtį, trauka gali pasikeisti reikšmingai,
tuo tarpu tiek pat pajudinus priešingoje spiečiaus pusėje esančią
žvaigždę trauka išlieka beveik tokia pati. Todėl skaičiuodami
vieną žvaigždę veikiančias jėgas, daugelio tolimų žvaigždžių
poveikį galime aproksimuoti, jas suvidurkindami. Toks metodas
vadinamas medžio algoritmu: visą spiečiaus užimamą erdvę
(kamieną) daliname į aštuonias kubines zonas (šakas), kiekvieną
iš jų – dar į aštuonias, ir taip toliau, kol kiekviename kube
lieka tik po vieną dalelę (lapą). Tada nagrinėdami konkrečią
dalelę veikiančias jėgas, galime žiūrėti nebe į pavienes kitas
žvaigždes, o į ištisas medžio šakas ir vidurkinti visų vienoje
šakoje esančių žvaigždžių poveikį. Kur brėžiame ribą tarp
artimų ir tolimų žvaigždžių, kitaip tariant, kaip toli esančias
žvaigždes nagrinėjame tik kartu su visa šaka, o ne atskirai,
priklauso nuo norimo tikslumo. Medžio algoritmas sumažina
reikalingų jėgos skaičiavimų kiekį nuo
); milijonas ir skaičiuojamų jėgų. Dešimties tūkstančių
žvaigždžių spiečiuje jėgų skaičiuoti reikėtų jau šimtą
milijonų – šimtą kartų daugiau. Bet paimkime vieną konkrečią
žvaigždę ir panagrinėkime, kaip ją veikianti jėga priklauso nuo
kitų žvaigždžių padėčių. Jei truputį pakeistume arti
esančios kaimynės padėtį, trauka gali pasikeisti reikšmingai,
tuo tarpu tiek pat pajudinus priešingoje spiečiaus pusėje esančią
žvaigždę trauka išlieka beveik tokia pati. Todėl skaičiuodami
vieną žvaigždę veikiančias jėgas, daugelio tolimų žvaigždžių
poveikį galime aproksimuoti, jas suvidurkindami. Toks metodas
vadinamas medžio algoritmu: visą spiečiaus užimamą erdvę
(kamieną) daliname į aštuonias kubines zonas (šakas), kiekvieną
iš jų – dar į aštuonias, ir taip toliau, kol kiekviename kube
lieka tik po vieną dalelę (lapą). Tada nagrinėdami konkrečią
dalelę veikiančias jėgas, galime žiūrėti nebe į pavienes kitas
žvaigždes, o į ištisas medžio šakas ir vidurkinti visų vienoje
šakoje esančių žvaigždžių poveikį. Kur brėžiame ribą tarp
artimų ir tolimų žvaigždžių, kitaip tariant, kaip toli esančias
žvaigždes nagrinėjame tik kartu su visa šaka, o ne atskirai,
priklauso nuo norimo tikslumo. Medžio algoritmas sumažina
reikalingų jėgos skaičiavimų kiekį nuo ![]() iki
iki ![]() .
Tūkstančio žvaigždžių spiečiuje skaičiuojamų jėgų sumažėja
nuo milijono iki 3000, dešimties tūkstančių žvaigždžių –
nuo šimto milijonų iki 40000. Na, iš tiesų skaičiavimų yra šiek
tiek daugiau, nes reikia nepamiršti tų artimų kaimyninių
žvaigždžių, kurios nėra vidurkinamos, bet resursų sutaupoma
tikrai daug.
.
Tūkstančio žvaigždžių spiečiuje skaičiuojamų jėgų sumažėja
nuo milijono iki 3000, dešimties tūkstančių žvaigždžių –
nuo šimto milijonų iki 40000. Na, iš tiesų skaičiavimų yra šiek
tiek daugiau, nes reikia nepamiršti tų artimų kaimyninių
žvaigždžių, kurios nėra vidurkinamos, bet resursų sutaupoma
tikrai daug.

Kamuolinis spiečius NGC 1866. Šaltinis: NASA / ESA / Hubble
Yra ir kitas būdas pagreitinti jėgų skaičiavimus: naudoti specialiai šiam procesui skirtus procesorius. 1989-2001 metais daugiausiai Japonijoje buvo vystomas projektas GRAPE: kuriami procesoriai, skirti būtent gravitacijos jėgų skaičiavimui. Vėliau mokslininkai pastebėjo, kad tą patį, ką ir GRAPE procesoriai, gali padaryti ir vaizdo plokštės – GPU. Prasidėjo bendrosios paskirties GPU (General Purpose Graphics Processing Unit, arba GPGPU) modelių era. Šie procesoriai jėgas, veikiančias N-kūnų modeliuose, skaičiuoja apie šimtą kartų greičiau, nei įprasti procesoriai (CPU), o to dažnai užtenka, kad būtų galima efektyviai skaičiuoti žvaigždžių spiečiaus evoliuciją. Būtent žvaigždžių spiečiams GPGPU labiausiai ir reikalingi, nes šiose sistemose žvaigždės susispietusios tankiai ir joms sunku taikyti medžio algoritmą. Tuo tarpu nagrinėjant didesnes ir retesnes sistemas, medžio algoritmas duoda puikius rezultatus ir tiesioginio jėgų skaičiavimo galima atsisakyti.
Didesnės už kamuolinius spiečius sistemos yra galaktikos ar jų telkiniai. Čia, žinoma, svarbų vaidmenį atlieka ir dujos, kurių judėjimui sekti neužtenka skaičiuoti vien gravitacijos. Bet didžiąją masės dalį Visatoje, kaip žinome, sudaro tamsioji materija, kuri – mūsų laimei ir patogumui – yra veikiama vien tik gravitacijos. Taigi dar prieš keletą dešimtmečių astronomai sugalvojo, kad N-kūnų modelius galima pritaikyti ir Visatos struktūrų evoliucijai tirti. Modelyje būtų skaičiuojama tik tamsiosios medžiagos evoliucija, o įprasta materija, manyta, turėtų sekti tamsiosios pėdomis.

Dailininko vizualizacija, kaip mūsų Galaktika atrodo kartu su tamsiosios materijos halu. Regimoji Galaktikos dalis – baldžas, diskas ir visa, kas telpa juose – yra iliustracijos centre, o ją gaubia melsvai pažymėtas tamsiosios materijos halas. Šaltinis: ESO/L Calçada
Maždaug šio amžiaus pradžioje sukurtas ne vienas kosmologinis skaitmeninis tamsiosios materijos modelis. „Kosmologinis“ čia reiškia, kad tiriamas pakankamai didelis erdvės regionas, jog tokiais masteliais Visatą galime laikyti tolygia. Grubiau tariant, regionas turi būti didesnis už didžiausius galaktikų telkinius. Kelių šimtų megaparsekų kraštinės ilgio kubas tam puikiai tiko. Ir sulaukėme – Millennium simulation 2005 metais, Bolshoi ir Horizon 2011-aisiais, Deus 2012-aisiais. Tai nebuvo pirmieji panašūs modeliai, tačiau patys didžiausi ir detaliausi. Kai kurie iš jų sekė daugiau nei šimtų milijardų dalelių judėjimą. Detaliausi iš šių modelių pasiekdavo kelių milijardų Saulės masių raišką; kitaip tariant, jie pajėgdavo išskirti ne tik Paukščių Tako, bet ir kai kurių palydovinių galaktikų, pavyzdžiui Magelano debesų, halus.
Kosmologinių modelių rezultatai davė daug žinių apie struktūrų formavimąsi ir vystymąsi Visatoje. Jie parodė, kaip iš mažyčių tankio netolygumų pirmykštėje Visatoje susiformuoja šiandien stebimi galaktikų spiečiai. Taip pat jie atskleidė, kad spiečius ir galaktikas jungia gijos, pramintos kosminiu voratinkliu, kurios buvo nematomos to metu teleskopams. Jose esančios retos karštos dujos tiesiogiai aptiktos tik pastaraisiais metais.

Vienas iš svarbių kosmologinių modelių rezultatų – tamsiosios materijos halų masių funkcija, t. y. skirtingos masės halų koncentracija Visatos erdvėje. X-ai žymi skaitmeninių modelių rezultatus skirtingomis Visatos evoliucijos stadijomis (z=0 yra dabartis, z=10 atitinka 500 mln. metų po Didžiojo sprogimo), skirtingų spalvų linijos – įvairias analitines funkcijas. Šaltinis: Lapi et al. 2013, Astrophysical Journal
Ir dar modeliai davė rezultatus, visiškai nesutampančius su stebėjimų duomenimis. Sumodeliuotų mažų galaktikų halų buvo gerokai per daug, lyginant su Paukščių Tako aplinka: pagal juos, mūsų Galaktika turėtų turėti apie tūkstantį palydovių, o ne kelias dešimtis. Net ir atskirose galaktikose medžiagos pasiskirstymas buvo neteisingas – centruose gerokai didesnis, nei rodo stebėjimai. Kurį laiką šie neatitikimai buvo laikomi didelėmis standartinio kosmologinio modelio problemomis. Bet per pastarąjį dešimtmetį problemos išnyko, kai po truputį N-kūnų modelius išstūmė modeliai, įtraukiantys ir dujų judėjimą bei jas veikiančius procesus, tokius kaip spinduliuotė, žvaigždžių sprogimai, galaktikų branduolių aktyvumas, smūginės bangos ir kita. Bet šių modelių pristatymą paliksiu kitam straipsniui.

Viena iš tamsiosios materijos kosmologinių modelių klaidų – trūkstamų palydovų problema. Grafike vaizduojamas palydovinių galaktikų skaičius priklausomai nuo jų sukimosi greičio (jis didėja, augant masei). Dvi pilkos linijos žymi skaitmeninių modelių rezultatus Paukščių Takui ir Andromedai, žalsva ir violetinė linijos – modelių, įtraukiančių dujų procesus, rezultatus toms pačioms galaktikoms. Raudoni apskritimai – realios Paukščių Tako palydovinės galaktikos. Matome, kad tamsiosios materijos modeliai prognozuoja daug daugiau mažų palydovų, nei yra iš tikrųjų, tačiau pridėjus dujas, modelių rezultatai tampa daug artimesni realybei. Juoda ir mėlyna linijos vaizduoja analogiškus modelių rezultatus didesnei galaktikai. Šaltinis: Sawala et al. (2014)
Laiqualasse

Kuomet paminėjai skaitmeninius modelius prieš atsirandant kompiuteriams truputį sutrikau. Bet paskui paskaitęs anglų kalba, supratau, kad problema, jog lietuvių kalboje digital ir numerical verčiasi į tą patį. Gal versti tiesiog matematinis modelis?
Bet matematinis modelis – irgi ne tas pats. Diskretizuotas modelis?
Kuriant kosmologinius skaitmeninius modelius, kaip suprantu yra įvedami dabartiniai parametrai ir paleidžiama simuliacija laiko tiesėje atgal? Cool, niekada nesusimasčiau, nors elementaru, kad N-kūnų modeliu laiko tiesėje galime ne tik į priekį bet ir atgal keliauti. Ir pasižiūrėti iš kur viskas atėjo ir kaip atrodė praeityje.
Ne, pradinės sąlygos kosmologiniams modeliams sukuriamos remiantis kosminės foninės spinduliuotės stebėjimais ir tiesine ten matomų netolygumų ekstrapoliacija. Netolygumai daugmaž tiesiškai auga pirmus keliasdešimt milijonų metų, taigi dažniausiai kosmologiniai modeliai prasideda nuo z=30 (100 mln. m. po Didžiojo sprogimo).
Modeliuoti juos laike atgal gali atrodyti įdomu, bet problema yra tos pačios paklaidos ir visokie statistiniai procesai. Tai pradėję nuo šiandieninių sąlygų atkurti praeities nelabai galėsime. Bet galime, suskaičiavę modelį, nustatyti, kiek jis skiriasi nuo šiandien stebimų Visatos savybių ir nagrinėti, kokie procesai nulemia tuos neatitikimus.