Praėjo kiek daugiau nei dveji metai nuo pirmojo gravitacinių bangų signalo aptikimo. Per tą laiką LIGO detektoriai JAV užfiksavo dar keturis signalus, o paskutinius du stebėti jiems padėjo ir Virgo konsorciumo detektorius Italijoje. Stebėjimas trim detektoriais leido žymiai tiksliau nustatyti šaltinių padėtis danguje – nuo poros tūkstančių kvadratinių laipsnių galimas plotas sumažėjo iki poros dešimčių. Kuo trečio detektoriaus atsiradimas taip padėjo aiškinantis šaltinių padėtis?

Atsakymas slypi protingame žodyje „trianguliacija“. Tai procesas, kuris leidžia GPS sistemoms nustatyti jūsų buvimo vietą, o prieš beveik du šimtmečius padėjo labai tiksliai išmatuoti Žemės dydį.

Jau iš pavadinimo galima suprasti, kad procesas kažkaip susijęs su trikampiais. Trikampiai turi tokią puikią savybę, jog nusibrėžę vieną trikampio kraštinę ir žinodami kitų dviejų ilgius, galime tiksliai pasakyti, kur yra trečioji trikampio viršūnė. O jei turime visų trijų viršūnių padėtis arba visų trijų kraštinių ilgius, galime tiksliai apskaičiuoti visus trikampio kampus. Ir panašiai. Šios geometrinės savybės leidžia išnaudoti trikampius įvairių nepasiekiamų daiktų padėčiai nustatyti.

Vienas paprastas trianguliavimo uždavinys dažnai sutinkamas mokykloje, trigonometrijos pamokose. Įsivaizduokite, kad esate prie upės ir norite nustatyti jos plotį, bet perplaukti upės negalite. Priešingame krante auga medis, kurį galite panaudoti kaip atskaitos tašką. Tada jums tereikia nusibrėžti liniją tame upės krante, kuriame esate, ir pamatuoti, kokia kryptimi matote medį iš vieno linijos galo ir iš kito. Taip gaunate trikampio kraštinę ir kitų dviejų kraštinių kryptis. Žinodami vienos kraštinės ilgį, galite apskaičiuoti ir kitų dviejų ilgius, o turint visą trikampį surasti jo aukštinę, kuri atitinka upės plotį, irgi nėra sudėtinga.

Panašiu principu rėmėsi ir Frydrichas Georgas Vilhelmas Struvė, vokiečių geografas, XIX amžiuje nusprendęs patikslinti Žemės spindulio matavimą. Tam jis pastatė 265 stulpus, nusidriekusius nuo Juodosios jūros pakrantės dabartinėje Moldovoje iki Arkties vandenyno krantų dabartinėje Norvegijoje. Stulpai buvo išdėstyti zigzagu taip, kad matuojant kryptis tarp jų buvo galima sudaryti daugybę trikampių. Trianguliacija leido nustatyti atstumus tarp trikampių taškų ir taip labai tiksliai išmatuoti atstumą tarp linijos galų. Žinodamas abiejų galų – Staro-Nekrasivkos pietuose ir Fulgeneso šiaurėje – Struvė apskaičiavo ir viso apskritimo, einančio per Žemės ašigalius, ilgį. Gautas rezultatas buvo patikslintas tik po šimto metų, XX amžiaus devintame dešimtmetyje, naudojant karinius palydovus.

GPS navigacija irgi veikia trianguliacijos principu, tik šiek tiek kitokiu – nebenaudojant kampų, bet labai tiksliai matuojant atstumus. GPS palydovai nuolatos siunčia informaciją padėties sekimo prietaisams, o šie prietaisai pagal signalų atkeliavimo laiką gali labai tiksliai nustatyti atstumą iki palydovų. Žinodamas atstumą bent iki trijų palydovų, prietaisas gali nustatyti savo padėtį tų palydovų atžvilgiu, o žinodamas palydovų padėtis danguje (ši informacija atsiunčiama su signalu) – savo absoliučią padėtį Žemės paviršiuje. Taigi jūsų telefone esanti galimybė sekti, kiek kilometrų nubėgote, nuvažiavote ar kitaip nukeliavote, ir kur apsilankėte, remiasi geru supratimu apie trikampius.

Gravitacinių bangų signalo atveju situacija yra panaši, kaip ir GPS, tik į sistemą reikėtų žiūrėti iš priešingos pusės. Mes žinome ant Žemės esančių objektų – detektorių – koordinates, ir norime nustatyti toli esančio objekto – gravitacinių bangų šaltinio – padėtį erdvėje. Tam mums reikia žinoti atstumą iki jo ir kryptį, kuria šaltinis yra dangaus skliaute. Atstumą nustatyti galima pagal signalo intensyvumą – tam iš principo užtektų vos vieno detektoriaus. Tik bėda, kad šio skaičiavimo paklaida yra daugybę kartų didesnė už Žemės skersmenį, taigi jos naudoti atstumų iki skirtingų detektorių skirtumams nustatyti neįmanoma. Bet tam galime panaudoti kitą informaciją – šiek tiek besiskiriančius signalo užfiksavimo laikus. Kiekvienas detektorius signalą užfiksuoja truputį kitu metu; tai reiškia, kad bangos frontas detektorių sudaromą plokštumą kerta kampu. Pavyzdžiui, jei signalas antrame detektoriuje užfiksuotas lygiai milisekunde vėliau, nei pirmame, tai tuo metu, kad banga ėjo pro pirmą detektorių, atstumas nuo jos fronto iki antrojo detektoriaus buvo 300 kilometrų (nes tiek šviesa, o ir gravitacinė banga, nueina per vieną milisekundę).

Turėdami informaciją iš dviejų detektorių, mes galime nustatyti kampą, kurį sudaro bangos frontas su linija, jungiančia detektorius. Jeigu atstumas tarp detektorių yra 3000 km, o bangos frontas, kaip aukščiau minėtame pavyzdyje, kerta vieną detektorių nuo kito būdamas 300 km atstumu, nesunku nusibraižyti statųjį trikampį, kurio viena kraštinė yra 300 km ilgio, o įžambinė – 3000 km (į bangos fronto kreivumą galime nekreipti dėmesio, nes šaltinis yra taip toli, kad nagrinėjamas bangos gabaliukas yra praktiškai tiesus). Tada galime nustatyti, kad gravitacinių bangų šaltinis yra tos 300 km ilgio kraštinės kryptimi.

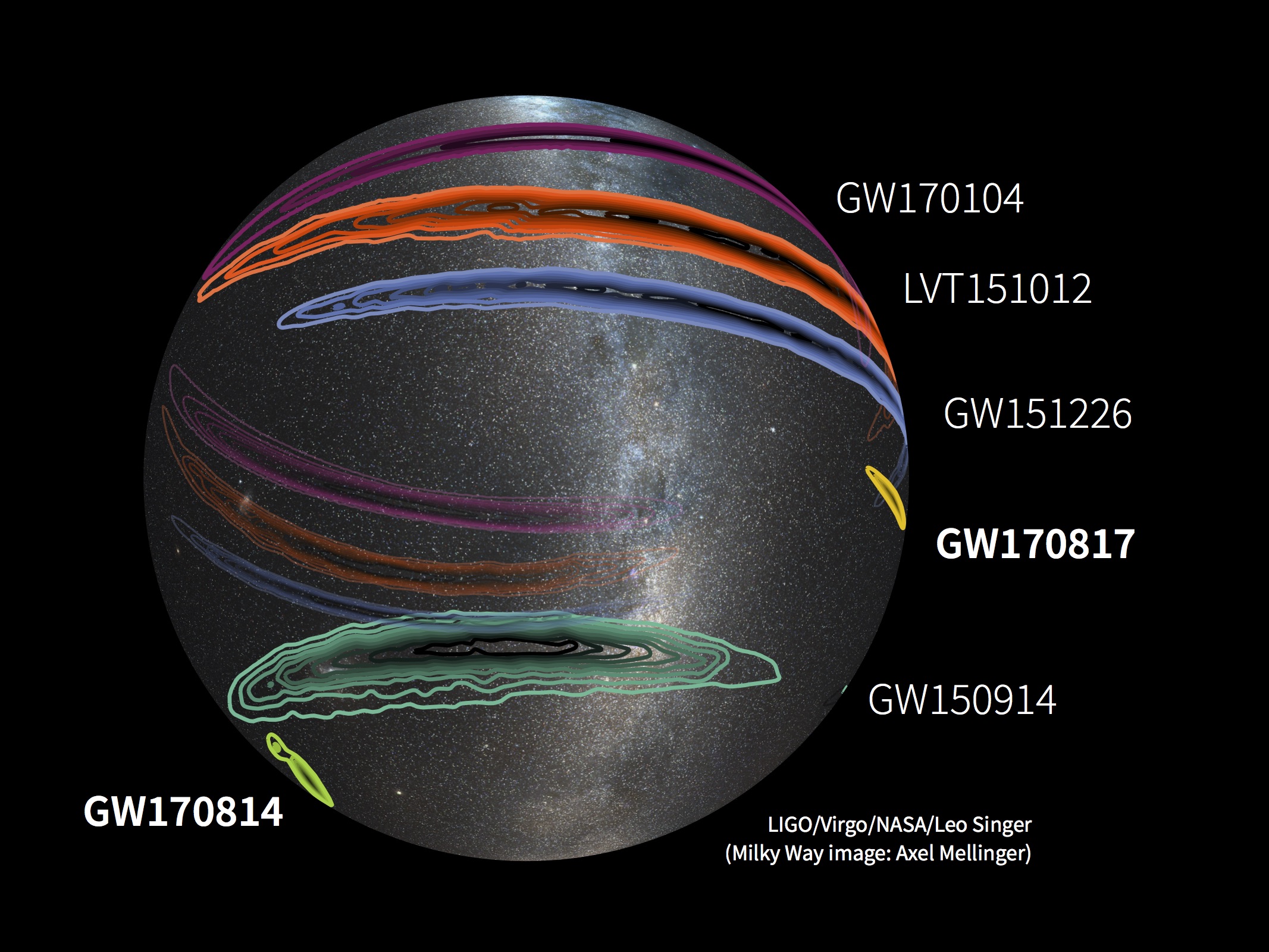
Tokio nustatymo problema – trečia dimensija. Vienas trikampis leidžia mums nustatyti šaltinio kryptį dviejuose matmenyse, tačiau nieko nepasako apie trečiąjį. Todėl pirmųjų signalų, kuriuos pagavo tik du LIGO detektoriai, lokalizacija dangaus skliaute buvo tokia „pailga“ – viena kryptimi padėtis nustatyta gana gerai, o kita – beveik visiškai neapibrėžta. Prisijungus trečiajam, Virgo, detektoriui, situacija pasikeitė iš esmės. Tarp trijų detektorių galima nubrėžti tris linijas ir, matuojant signalo aptikimo laiko skirtumus, kryptį nustatyti trijose plokštumose. Net dviejų nustatymų užtenka, kad šaltinio padėtis būtų apibrėžta gana tiksliai, o trečias matavimas dar patikslina rezultatą, sumažindamas jo paklaidas.

Jei detektorių būtų dar daugiau – o taip ir bus, kai įsijungs Indijoje ir Japonijoje statomieji, – šaltinių lokalizavimas dar pagerės. Ne tiek smarkiai, kiek pereinant nuo dviejų detektorių prie trijų, bet paklaidos vis tiek sumažės. Ir tada bus galima tiksliau ieškoti kiekvieno gravitacinių bangų šaltinio galimai skleidžiamų elektromagnetinių bangų, ar bent jau galaktikos, kuriame tas įvykis įvyko.

Laiqualasse