Paskutiniame Visatos kąsnelyje rašiau apie zondą Junoną, kuri keliauja Jupiterio link, bet tam tikslui turi pralėkti pro Žemę. Tokia iš pirmo žvilgsnio keista orbita išnaudoja efektą, vadinamą gravitacine svaidykle (angl. gravitational slingshot). Apie tai, koks tai efektas ir kaip jis padeda skrajojant pro Saulės sistemą, čia ir papasakosiu. Pasistengsiu aiškiai ir trumpai, o kaip pavyks – matysime.
Įsivaizduokite, kad skrendate kosminiu laivu. Tam kartui pamirškime visokius spinduliuotės ir mažos traukos kabinoje pavojus, ir tiesiog skriskime, atsiplėšę nuo Žemės paviršiaus į kosmosą. Lekiame tolyn nuo Saulės, bet matome, kad žvaigždės gravitacijai įveikti reikia baisingai daug kuro. Daugiau, nei tilpo į mūsų kuro bakus. Taigi kažkur pusiaukelėje iki Jupiterio kuras baigiasi, netrukus laivas sustoja ir ima lėtai, bet nenumaldomai kristi Saulės link.
Pražūtis? Nebūtinai! Vis dar galėdami daryti nedidelius manevrus laivo trajektoriją pakeiskime taip, kad jis pralėktų visai šalia Žemės. Ne atsitrenktų į ją, bet pakliūtų į tą erdvės dalį, kurioje Žemės trauka dominuoja (lyrinis nukrypimas – ši zona vadinama Hilo (Hill) sfera, nors jos forma nėra tiksliai sferinė). Artėdami prie Žemės skaičiuojame savo būsimą trajektoriją ir pasirenkame ją taip, kad į Žemės traukos zoną įkristume maždaug statmenai Žemės orbitai, o išlėktume lygiagrečiai, maždaug ta pačia kryptimi, kuria Žemė sukasi aplink Saulę. Taigi pasinaudodami Žemės gravitacija, kuri šiaip Saulės sistemoje yra visai nereikšminga, pasukome laivą 90 laipsnių kampu. Tai šiek tiek panašu į situaciją, kai bėgdami užsikabiname už kokio stulpo ar medžio, kad galėtume staigiai pasisukti; tik čia medžio vaidmenį atlieka Žemės trauka.
Kas gi atsitinka, atlikus tokį manevrą? Iš pradžių lėkėme Saulės link greičiu X; laikant, kad erdvėlaivis krito laisvai ir iš didelio atstumo, X yra maždaug 1,4 karto didesnis už Žemės orbitos greitį, taigi apie 42 kilometrus per sekundę. Žemės atžvilgiu taip pat judame panašiu greičiu; priklausomai nuo tikslios judėjimo krypties, santykinis greitis tarp erdvėlaivio ir Žemės gali būti ir mažesnis. Kaip ten bebūtų, judėjimo greitis smarkiai viršija pabėgimo iš Žemės traukos greitį, todėl Žemė mūsų nesulaiko, o tik pasuka. Judėjimo greitis Žemės atžvilgiu taip pat beveik nepakinta, tačiau judėjimo greitis Saulės atžvilgiu gali pakisti smarkiai. Taip yra todėl, kad posūkį atlikome ne aplink stacionarų „stulpą“, bet aplink judantį 30 km/s greičiu. Idealiu atveju, jei iš Žemės traukos zonos išlekiame lygiagrečiai Žemės judėjimui aplink Saulę, mūsų greitis nuo ~42 km/s padidėja iki 42+30 = 72 km/s. O tokio greičio jau per akis pakanka ne tik Jupiterį pasiekti, bet ir pabėgti iš Saulės sistemos.
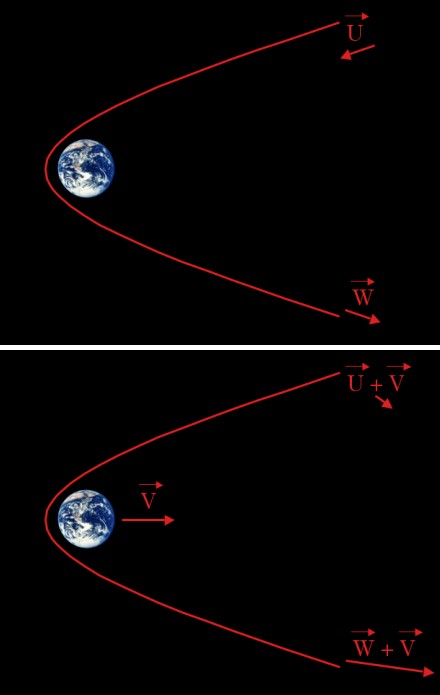
Štai tokia ir visa gravitacinio svaidymo esmė. Šnekant šiek tiek globaliau, mes pasinaudojame gravitacija ir atimame šiek tiek energijos iš Žemės orbitinio judėjimo, o tą energiją pridedame prie savo judėjimo. Aišku, erdvėlaivio masė yra tokia nykstamai maža, palyginus su Žemės mase, kad Žemės orbitai dėl tokio manevro poveikio praktiškai nėra. Bet jei panašų manevrą kartotume labai daug kartų, galima būtų pasiekti ir pastebimų rezultatų. Teko skaityti apie vieną grandiozišką pasiūlymą, kaip tolimoje ateityje Žemės gyventojai galėtų išvengti planetos perkaitimo (jis įvyks per artimiausius porą milijardų metų, nes Saulė po truputį kaista): pakinkyti asteroidą ir paleisti jį orbita (nuolat reguliuojama), kuria skrisdamas jis vis pralėktų šalia Žemės ir šalia Jupiterio. Teisingai parinkus trajektoriją, asteroidas galėtų „pavogti“ šiek tiek orbitos energijos iš Jupiterio ir perduoti ją Žemei kiekvienu praskridimu. Taip Žemė po truputį toltų nuo Saulės, kompensuodama Saulės įkaitimą.
Žinoma, realybėje gravitaciniai svaidymai nėra tokie efektyvūs, kaip aprašiau aukščiau. Svarbu teisingai parinkti trajektoriją, kad Žemės (ar kito kūno, kuris naudojamas sviedimui) trauka galėtų reikšmingai paveikti judėjimą, taip pat kad nebūtum nusviestas kita kryptimi, negu reikia. Visgi degalų santaupos, šitaip įgreitinant erdvėlaivius, yra milžiniškos, taigi beveik kiekviena tolimesnė misija naudojasi gravitacinėmis svaidyklėmis; abu Vojadžeriai pakeliui iš Saulės sistemos pagreitėjo pasinaudodami Jupiterio ir kitų planetų gravitacija. Erdvėlaivių trajektorijos, paleidimo ir variklių įjungimo bei išjungimo laikas planuojami bent keletą metų į priekį. Kalbant apie tokias misijas, dažnai naudojamas terminas „paleidimo langas“ (angl. launch window) – tai yra laiko tarpas, kada paleidus erdvėlaivį iš Žemės, jis galės tinkamai praskristi pro kitus Saulės sistemos kūnus (arba tą pačią Žemę) ir pasiekti savo kelionės tikslą. Praleidus paleidimo langą, kito gali tekti laukti metus ar net ilgiau, kol planetos vėl susidėlios į tinkamą konfigūraciją. Šiuo atžvilgiu kosminių misijų planuotojai šiek tiek primena kokius nors paslaptingus kultistus, kurie laukia tinkamos planetų padėties, kad galėtų iškviesti Ktulu ar kokį kitą Spagečių monstrą.

Tiesa, kartais net ir geriausias planetų išsidėstymas neleidžia nuskristi ten, kur norima. Tuomet tenka naudoti variklius viso skrydžio metu, kartais pagreitinant erdvėlaivį, kartais sulėtinant, kad būtų pataikoma į gravitacines svaidykles tokia kryptimi ir tuo metu, kaip reikalinga. Ir čia taip pat padeda gravitaciniai efektai. Čia svarbu tai, kad bet koks kūnas, judantis elipsine (ištęsta) arba hiperboline (t.y. tik pralekiantis pro šalį) trajektorija, juda tuo greičiau, kuo arčiau traukos centro yra. Judėjimo kinetinė energija proporcinga greičio kvadratui. Vadinasi, jei kosminis laivas padidina savo greitį dydžiu Y, tai jo kinetinė energija padidės labiau, jei pagreitėjimas įvyko esant arti traukos centro (prie didesnio judėjimo greičio pridėjus tą patį Y, baigtinio greičio kvadratas padidės labiau, nei Y pridėjus prie mažesnio greičio). Taigi jei jau reikia jungti variklius, naudingiausia juos įjungti lekiant pro pat gravitacinę svaidyklę. Tada net ir nedidelis greičio pokytis gali reikšmingai pakeisti likusią kelionę.
Tikiuosi, kad paaiškinau šitą reikalą suprantamai. Jeigu ne – klauskite ir piktinkitės, bandysiu taisytis.
Laiqualasse

Išties, labai įdomūs dalykai tos gravitacinės svaidyklės. Ar skaičiuojant visas šias trajektorijas naudojami two-body modeliai ar prisireikia three-body problem dalinių sprendinių?
Dar pridėsiu keletą įdomių faktų šia tema:
Cassini palydovo kelionėje naudojant šį būdą buvo sutaupyta 75 tonos raketinio kuro (neskaitant to, jog visas palydovas dar ir pasunkėtų su tokia mase, tad reiktų dar daugiau kuro). Aišku, norint taupyti kuro, reikia aukoti keliavimo laiką, kuris pailgėja (šiuo atveju – 7 metus ilgiau);
Voyager palydovo išsiuntimui naudotas planetų išsidėstymas kartojasi tik kas 175 metus.
O aš labai laukiu, kol pradės naudoti joninius variklius – turėtų supaprastėti/pagreitėti/atpigti palydovų kelionės :)
Aš tai laukiu, kol branduolinius variklius pradės naudoti :) Gal svajuko dramblionės, bet tikiuosi, kad taip kada nors bus.
Skaičiuojant trajektorijas naudojami ne dviejų ir ne trijų kūnų, o visos Saulės sistemos skaitmeniniai modeliai. Čia svarbus tikslumas, taigi ir kitų planetų įtaka trajektorijai turi būti įvertinta.
„Voyager palydovo išsiuntimui naudotas planetų išsidėstymas kartojasi tik kas 175 metus.“
Turbūt turi omeny Žemės, Jupiterio ir Saturno tarpusavio padėtis, ar ne? Nes jei kalbėtume apie visas planetas, tai tikrai ne kas 175 metus, o gerokai rečiau kažkiek panaši konfigūracija susidaro.
nereikia tu branduolinių. netolimoje ateityje užteks ir joninių arba paprastų cheminių. Svarbiausia yra pačiame vaakume sukurti infrastruktūrą: nuo kuro išgavimo ir perdirbimo iki kosminių aparatų statybos.
Cheminiai vis tiek siaubingai neefektyvūs. Aukštesnio masės-energijos konversijos efektyvumo norisi. Branduoliniai sprogimai pasiekia beveik 0,1%, tai jau labai daug. Termobranduolinėse reakcijose galime tikėtis 0,7%, tai būtų dar geriau.
girdėjau, kad tik prieš kelias dienas buvo pagaliau pasiektas termobranduolinės reakcijos naudingumo lygis: reakcijos išskirta energija pagaliau viršijo jai sukūrti panaudotą, taip kad mobilių reaktorių (erdvėlaiviams) manau šį amžių dar galime nelaukti, o branduolinius gal ir išvysime.
Nežinia, kaip su tais termobranduoliniais bus. Gal kai pagaliau bus pasiekta ekonominė nauda, jie ims tobulėti taip sparčiai, kad po keleto dešimtmečių tilps ir į kosminius laivus. Bet sutinku, kad tai mažai tikėtina.
Su branduoliniais varikliais yra viena bėda – tarptautinė sutartis dėl kosmoso nenaudojimo kariniams tikslams. Branduolinė energetika patenka po „kariniais tikslais“ :(
„manau šį amžių dar galime nelaukti, o branduolinius gal ir išvysime“
Liudną šypseną išspaudžiau :)